Main Content
Reversed Angles
I'll be standing in for Leon, as he seems to have a phobia of sin-1, cos-1 and tan-1. These functions are used for finding the angle in a triangle. Which can be terribly useful when you have to get an AI opponent to point a gun at your head. Although we won't be covering any Flash usage in this tutorial, most people will find it useful as a reference point. We shall start with an example.
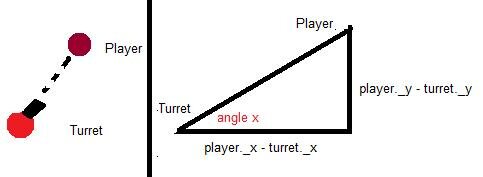
As you can see, the classic player and turret combination can be broken down into a triangle. One thing to note though, where I put player._x/y - turret_x/y may turn out to be negative, you should make it positive. The thing we actually want to find out though is angle x - that is to say the angle the turret needs to turn to if it wants to shoot the player.
Angle X can be found out fairly easily. Remember from the last tutorial where Leon said "tan A [in this case angle x] = O/A "? Well in this case the opposite is player._y - turret._y (eg. 5) and the adjacent is player._x - turret_x (eg 10).
So, in our case tan x = 5/ 10 (Don't get it? Reread the last paragraph/tutorial). The key thing we are going to learn today is inverse trigonometry. That is finding the angle (what we wanted all along). Luckily, Maths provides us a nifty way of doing this: x = tan-1(5/10). That is equal to tan-1(0.5). A quick turn on and dust down of the old calculator should tell us that angle x is.... actually, work it out for yourself. There you go, all done. Apart from the fact that Flash has a rather odd way of negating angles. Leon will cover that in a future tutorial.
Thanks for reading this,
Harry (26.565051177077989351572193720453 )





